Cục Khảo thí và kiểm định chất lượng giáo dục - Bộ Giáo dục - đào tạo vừa ấn hành tài liệu Cấu trúc đề thi tốt nghiệp THPT, thi tuyển sinh ÐH-CÐ 2009 theo chương trình THPT phân ban đại trà.
Ðây là tài liệu chính thức giúp giáo viên và HS chuẩn bị ôn luyện cho các kỳ thi sắp tới. Ngoài phần cấu trúc đề, nội dung kiến thức yêu cầu với từng đề thi, từng môn, bộ sách còn có phần so sánh điểm giống và khác nhau giữa sách giáo khoa theo chương trình chuẩn và chương trình nâng cao từng môn học và một số đề thi minh họa. CẤU TRÚC ĐỀ THI TỐT NGHIỆP MÔN TOÁN
* Phần chung dành cho tất cả thí sinh:
Câu I (3 điểm):
- Khảo sát, vẽ đồ thị của hàm số.
- Các bài toán liên quan đến ứng dụng của đạo hàm và đồ thị của hàm số: chiều biến thiên của hàm số, cực trị, tiếp tuyến, tiệm cận (đứng và ngang) của đồ thị hàm số. Tìm trên đồ thị những điểm có tính chất cho trước, tương giao giữa hai đồ thị (một trong hai đồ thị là đường thẳng)…
Câu II (3 điểm):
- Hàm số, phương trình, bất phương trình mũ và lôgarit.
- Giá trị lớn nhất và nhỏ nhất của hàm số. Tìm nguyên hàm, tính tích phân.
- Bài toán tổng hợp.
Câu III (1 điểm):
Hình học không gian (tổng hợp): tính diện tích xung quanh của hình nón tròn xoay, hình trụ tròn xoay; tính thể tích khối lăng trụ, khối chóp, khối nón tròn xoay, khối trụ tròn xoay; tính diện tích mặt cầu và thể tích khối cầu.
* Phần riêng (3 điểm):
Thí sinh học chương trình nào chỉ được làm phần dành riêng cho chương trình đó.
1. Theo chương trình chuẩn:
Câu IV.a (2 điểm):
Nội dung kiến thức:
- Xác định tọa độ của điểm, vectơ.
- Mặt cầu.
- Viết phương trình mặt phẳng, đường thẳng.
- Tính góc, tính khoảng cách từ điểm đến mặt phẳng. Vị trí tương đối của đường thẳng, mặt phẳng và mặt cầu.
Câu V.a (1 điểm):
Nội dung kiến thức:
- Số phức: môđun của số phức, các phép toán trên số phức. Căn bậc hai của số thực âm. Phương trình bậc hai hệ số thực có biệt thức ∆ âm.
- Ứng dụng của tích phân: tính diện tích hình phẳng, thể tích khối tròn xoay.
2. Theo chương trình nâng cao:
Câu IV.b (2 điểm):
Nội dung kiến thức:
Phương pháp tọa độ trong không gian:
- Xác định tọa độ của điểm, vectơ.
- Mặt cầu.
- Viết phương trình mặt phẳng, đường thẳng.
- Tính góc; tính khoảng cách từ điểm đến đường thẳng, mặt phẳng; khoảng cách giữa hai đường thẳng. Vị trí tương đối của đường thẳng, mặt phẳng và mặt cầu.
Câu V.b (1 điểm):
Nội dung kiến thức:
- Số phức: Môđun của số phức, các phép toán trên số phức. Căn bậc hai của số phức. Phương trình bậc hai với hệ số phức. Dạng lượng giác của số phức.
Ðồ thị hàm phân thức hữu tỉ dạng y =(ax2 + bx +c)/(px+q)
và một số yếu tố liên quan.
- Sự tiếp xúc của hai đường cong.
- Hệ phương trình mũ và lôgarit.
- Ứng dụng của tích phân: tính diện tích hình phẳng, thể tích khối tròn xoay.
CẤU TRÚC ĐỀ THI ĐẠI HỌC - CAO ĐẲNG MÔN TOÁN Đề thi toán kỳ thi ĐH 2009, phần chung dành cho tất cả thí sinh chiếm 7 điểm. Phần riêng (gồm 2 câu) chiếm 3 điểm. Đề thi yêu cầu nhiều kiến thức mở rộng hơn so với kỳ thi tốt nghiệp.
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm)
Câu I (2 điểm):
- Khảo sát, vẽ đồ thị của hàm số.
- Các bài toán liên quan đến ứng dụng của đạo hàm và đồ thị của hàm số: chiều biến thiên của hàm số. Cưc trị. Giá trị lớn nhất và nhỏ nhất của hàm số. Tiếp tuyến, tiệm cận (đứng và ngang) của đồ thị hàm số. Tìm trên đồ thị những điểm có tính chất cho trước, tương giao giữa hai đồ thị (một trong hai đồ thị là đường thẳng)…
Câu II (2 điểm)
- Phương trình, bất phương trình, hệ phương trình đại số.
- Công thức lượng giác, phương trình lượng giác.
Câu III (1 điểm)
- Tìm giới hạn.
- Tìm nguyên hàm. Tính tích phân.
- Ứng dụng của tích phân: tính diện tích hình phẳng, thể tích khối tròn xoay.
Câu IV (1 điểm)
Hình học không gian (tổng hợp): quan hệ song song, quan hệ vuông góc của đường thẳng, mặt phẳng. Tính diện tích xung quanh của hình nón tròn xoay, hình trụ tròn xoay; tính thể tích khối lăng trụ, khối chóp, khối nón tròn xoay, khối trụ tròn xoay; tính diện tích mặt cầu và thể tích khối cầu.
Câu V. Bài toán tổng hợp (1 điểm)
II. PHẦN RIÊNG (3 điểm)
Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc phần 2).
1. Theo chương trình chuẩn:Câu VI.a (2 điểm):
Nội dung kiến thức: phương pháp tọa độ trong mặt phẳng và trong không gian.
- Xác định tọa độ của điểm, vectơ.
- Đường tròn, elip, mặt cầu.
- Viết phương trình mặt phẳng, đường thẳng.
- Tính góc, tính khoảng cách từ điểm đến mặt phẳng. Vị trí tương đối của đường thẳng, mặt phẳng và mặt cầu.
Câu VII.a (1 điểm)
Nội dung kiến thức:
- Số phức.
- Tổ hợp. xác suất, thống kê.
- Bất đẳng thức. Cực trị của biểu thức đại số.
2. Theo chương trình nâng cao:Câu VI.b (2 điểm)
Phương pháp tọa độ trong mặt phẳng và trong không gian:
- Xác định tọa độ của điểm, vectơ.
- Đường tròn, ba đường conic, mặt cầu.
- Viết phương trình mặt phẳng, đường thẳng.
- Tính góc; tính khoảng cách từ điểm đến đường thẳng, mặt phẳng; khoảng cách giữa hai đường thẳng. Vị trí tương đối của đường thẳng, mặt phẳng và mặt cầu.
Câu VII.b (1 điểm)
Nội dung kiến thức:
- Số phức.
- Đồ thị hàm phân thức hữu tỉ dạng y = (ax^2 + bx + c )/( px + q) và một số yếu tố liên quan.
- Sự tiếp xúc của hai đường cong.
- Hệ phương trình mũ và lôgarit.
- Tổ hợp, xác suất, thống kê.
- Bất đẳng thức. Cực trị của biểu thức đại số.
(Nguồn: Tài liệu Cấu trúc Đề các môn thi tốt nghiệp, ĐH-CĐ 2009 –
Cục Khảo thí và Kiểm định chất lượng giáo dục –
Bộ Giáo dục và đào tạo)
. Cho 
ta được:
. Do đó: 
là một số thực.
. Nếu 
là hữu tỉ.
2. Công thức Gauss:
3. Công thức Leibnitz:
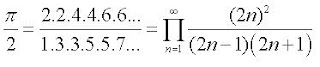5. Công thức Viete: 
Ngoài ra, còn có một số công thức rất nổi tiếng liên quan đến PI 
. Suy ra
và ứng dụng", đăng trên báo THTT số tháng 8 năm 2007, của thầy Đỗ Thanh Hân.
,
,
. Khi đó:
, tức đó suy ra đẳng thức cần chứng minh.
